Report: Interleaving Effect

Introduction

This report on cognitive science to enhance instruction will focus on Rohrer, Dedrick, & Burgess‘s 2014 study, “The benefit of interleaved mathematics practice is not limited to superficially similar kinds of problems”. Traditionally, when teaching a subject, the subject is broken into small blocks. We instruct students to master solving problems in each smaller block before moving on to the next block. This is called blocking. An example of this would be a traditional math class: we master addition and subtraction before moving on to multiplication. In Interleaving, one “mixes, or interleaves, practice on several related skills together…For instance, a pianist alternates practice between scales, chords, and arpeggios, while a tennis player alternates practice between forehands, backhands, and volleys” (Pan, 2015). I chose this particular article on interleaving because of its focus on teaching math. As an electrical instructor, I use math to describe what is happening in a circuit, and I believe there are a lot of parallels in teaching math and teaching circuits.

Reliability of article

I believe this article (Rohrer et al., 2014) to be an exceptionally reliable source for information on interleaving practice. The primary author, Doug Rohrer is a professor at the University of South Florida. He holds a B.S. in Mathematics and a M.A., Ph. D. in Psychology. I believe these qualifications make him an excellent person to assess the effectiveness of interleaving practice in teaching math skills.

This paper, published in 2014, presents the findings of a study performed on 140 grade 7 students using both blocked and interleaved practice to teach mathematics. The study was well designed, ensuring that neither blocked nor interleaved practice had an advantage. The conclusion of this study was an astonishing 72% success rate for interleaved practice over 38% success for blocked practice. The authors go on to reference “four previously-published studies [that] have compared the effects of interleaved and blocked mathematics practice (Le Blanc & Simon, 2008; Mayfield & Chase, 2002; Rohrer & Taylor, 2007; Taylor & Rohrer, 2010).” (Rohrer et al., 2014, p. 3). These four studies similarly concluded that interleaved practice outperforms blocked practice.

Principles of Interleaving

Fundamentally, interleaving is the process of consciously practicing a subject, moving onto a different subject, then coming back to the original subject to reinforce the learning. One key principle of interleaving is the development of discrimination. Problem discrimination is the act of determining which type of problem is being asked, prior to being able to go through the method of solving it. Typically, once a student identifies a strategy to solve the type of problem being taught in block practice, they can keep re-applying the same methodology to all the problems presented until finished that block. Conversely, in interleaving practice, random problems are given in no particular order. Students must determine which strategy is appropriate to solve the problem, then go about solving it.

This leads to the second key principle of interleaving: By constantly challenging the student to determine which strategy is needed to solve a problem, we are “strengthening the association between each kind of problem and its corresponding strategy” (Rohrer et al., 2014, p. 1).

While discussing principles of the interleaving effect, we must not discount spacing effect. “Spacing Effect states that we learn material more effectively and easily when we study it several times spaced out over a longer time span, rather than trying to learn it in a short period of time” (Spacing Effect, n.d.). Interleaving naturally incorporates spacing effect by spreading out the learning. In effect, interleaving can be thought of as learning multiple subjects simultaneously utilizing spacing effect.

Application of Interleaving

Interleaving has been proven effective in teaching math. I intend to use interleaving to teach combination circuit analysis, which requires the use of math formulas and following current flow. Traditionally, students learn how to solve series circuits, followed by parallel circuits, then learn how to do combination circuits which incorporate elements of both series and parallel connections. The new way I intend to teach this would be as follows:

Initially the path would not diverge from typical blocking practice. I would introduce series circuits by use of schematics and giving the laws of solving series circuits.

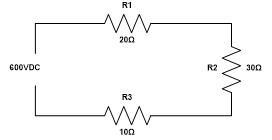Laws for Series Circuits Rt = R1 + R2 + R3 … It = I1 = I2 = I3 … Et = E1 + E2 + E3 … Pt = P1 + P2 + P3 …

Next, I would introduce parallel circuits:

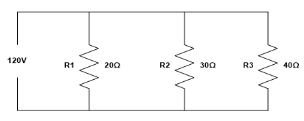Laws for Parallel Circuits 1/Rt = 1/R1 + 1/R2 + 1/R3 … It = I1+I2+I3… Et = E1 = E2 = E3… Pt = P1+P2+P3…

After basic comprehension of series and parallel connections, I would move straight into simple combination circuits:

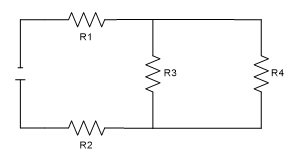
Steps to Solve Combination Circuits 1) Identify which resistors are in series and parallel 2) Simplify circuit by replacing the series and parallel resistors in step (1) with an equivalent resistor and re-draw. May be necessary to do multiple times. Work towards the voltage source! 3) Solve for Rt with substitute equivalent resistances 4) Solve for It 5) Use Kirchhoff’s current and voltage laws to solve rest of circuit, working away from the voltage source.

After some basic practice on mastering solving combination circuits, I would spend the next couple days reinforcing this knowledge in the lab building circuits, and doing interleaved worksheets which contain series, parallel, and combination circuit problems. These worksheets would also have word problems designed to get students to think about the basic laws of series and parallel circuits. An example word problem might be:

Three resistors (R1, R2, R3) are connected in series. Their total resistance (Rt) equals 40 ohms. If 120V is applied, what is the current flowing through R2?

I believe by strongly reinforcing the basic laws of series and parallel circuits through interleaving, students will have a much easier time grasping combination circuit analysis. The next logical step would be to continue the interleaving process and introduce practical applications of series and parallel circuits such as a voltage dividers and Wheatstone bridges.

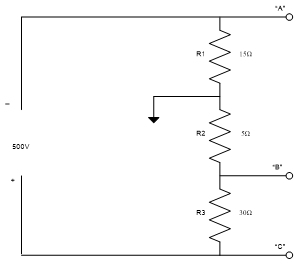
Voltage divider (basic series circuit)

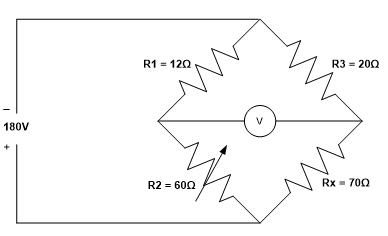
Wheatstone bridge (simple combination circuit)

By interleaving these applications with problems of basic circuit analysis, I hope to strengthen the association of series and parallel laws with respect to application style problems.

References

Pan, S. C. (2015). The Interleaving Effect: Mixing It Up Boosts Learning. Scientific American. Retrieved from: https://www.scientificamerican.com/article/the-interleaving-effect-mixing-it-up-boosts-learning/

Rohrer, D., Dedrick, R. F., & Burgess, K. (2014). The benefit of interleaved mathematics practice is not limited to superficially similar kinds of problems. Psychonomic Bulletin & Review, 21, 1323-1330.

Spacing Effect. (n.d.). In Alleydog.com’s online glossary. Retrieved from: http://www.alleydog.com/glossary/definition-cit.php?term=Spacing Effect